2020. 8. 12. 00:08ㆍ데이터 분석 기본
우리는 앞선 포스팅(https://direction-f.tistory.com/28)에서 두 가지의 가설을 정의하였습니다. 하나는 우리가 주장하고자 하는 가설(대립가설, H1)이고, 다른 하나는 그 주장을 입증할 수 없을 때 주장을 무효화하면서 받아들여야 하는 가설(귀무가설, H0)입니다.
그렇다면 우리는 어떤 가설을 받아들여야 하는지 어떻게 결정할 수 있을까요? 이 때 활용하는 것이 검정통계량(Test statistic)입니다.
[검정통계량]
다시 앞의 포스팅의 예를 들어보도록 하겠습니다. 우리는 아래와 같이 가설을 수립했습니다.
대립가설(H1) : 다이어트 프로그램은 초등학생들의 평균 몸무게를 줄였을 것이다(μ<70)
귀무가설(H0) : 다이어트 프로그램은 평균 몸무에게 영향을 미치지 못했다.(μ=70)
대립가설을 채택하기 위해서는 다이어트 후 남자 초등학생의 평균 몸무게(표본평균)가 70에 비해 상당히 적어야 합니다. 즉, 어떤 적당한 값에 대해 그 값보다 적을 때 귀무가설을 기각하게 됩니다.
이렇게 표본평균이 취하는 구간중에 H0를 기각하게 하는 구간을 기각역(critical region)이라고 합니다. 이를 아래와 같이 표현합니다. 중요한 것은 적절한 값 c를 정하는 것입니다.

우리는 표본만을 관측하여 가설에 대해 검정하기 때문에 오류가 발생할 확률이 항상 존재합니다. 1종 오류를 범할 확률을 α, 2종 오류를 범할 확률을 β라고 하겠습니다. 두가지 종류의 오류를 함께 최소화하는 기각역을 구하면 가장 바람직하겠지만, α와 β는 반대로 움직입니다. 즉 α를 줄이면 β가 커지게 되고, α가 커지게 되면 β는 줄어들게 됩니다.
여기서 α와 β는 아래와 같이 표현됩니다.

보통의 경우 1종 오류가 2종 오류보다 심각한 것이기 때문에 1종 오류를 범할 확률을 작게 가져갑니다. 그래서 일반적으로 α값을 0.05나 0.1로 정하게 되고 이 때 정한 α값을 유의수준(Sigmificance level)이라고 합니다. 그리고 이 유의수준에 맞춰 c를 결정하게 됩니다.
[Z 검정]
표본평균은 아래와 같은 방법을 이용하여 표준화 시킬 수 있습니다.(만약 모집단의 표준편차를 모르면, 표본의 표준편차를 사용해도 무방합니다.)

이 때 유의수준 α에 대하여 기각역 R은 아래와 같습니다.

일반적으로는, 표본으로부터 직접 Z를 구하여 기각역을 구하는 것이 흔합니다. 따라서 기각역을 다시 아래와 같이 표현합니다.

위와 같은 검정를 Z-검정( Z-test)라고 합니다.
이제까지는 대립가설이 μ<x 경우에만 고려했습니다. 우리는 μ>x 인 경우, 그리고 μ≠x 인 경우 모두 고려할 수 있습니다. 검증형태는 아래와 같이 정리될 수 있습니다.
표본의 크기가 클 때 모평균 μ에 대한 가설 H0: μ=x를 검정하기 위한 검정통계량은 아래와 같습니다.

각 기각역은 아래와 같습니다.
| 단측검정(μ<x) |  |
| 단측검정(μ>x) | 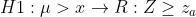 |
| 양측검정 |  |
파이썬을 활용해서 기각여부를 판단해보겠습니다.
from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
## 다이어트 전 비만 남자 초등학생의 몸무게 평균이 70, 표준편차가 3라고 가정
## 대립가설(H1) : 다이어트 프로그램은 초등학생들의 평균 몸무게를 줄였을 것이다(μ<70)
## 귀무가설(H0) : 다이어트 프로그램은 평균 몸무에게 영향을 미치지 못했다.(μ=70)
## 30명만 추출하여 다이어트 후의 효과를 검증하고자 함(임의로 Random sampling)
sample_data=np.random.randint(60,75,30)##low, high, size
sample_mean = np.mean(sample_data)
sample_std = np.std(sample_data, ddof=1)
## 검정을 위한 통계량 계산
Z_statistic = (sample_mean -70)/(sample_std/np.sqrt(30))
## -Z_0.5 계산
mu2 = 0
std2 = 1
standard_norm = norm(mu2,std2)
z_05=-standard_norm.ppf(0.95) ## α=0.05일때
## 기각여부 판단
if Z_statistic <= z_05:
print("H0 기각")
else :
print("H0 채택")
## 기각역 시각화
x = np.linspace(standard_norm.ppf(0.01), standard_norm.ppf(0.99),1000)
z = np.linspace(-2.5,z_05,1000)
plt.plot(x, standard_norm.pdf(x),'r-', lw=2, alpha=0.3, label='norm pdf')
plt.vlines(z_05, 0, standard_norm.pdf(z_05), colors="g")
plt.fill_between(z, 0,standard_norm.pdf(z), color ="g", alpha=0.3)
plt.title("standard normal distribution")
plt.legend()
plt.show()

'데이터 분석 기본' 카테고리의 다른 글
| 두 모집단의 비교(표본이 클 때) (0) | 2020.08.20 |
|---|---|
| 가설검정 > P-value(유의확률) (0) | 2020.08.13 |
| 가설검정 > 가설, 검정통계량 (0) | 2020.08.09 |
| 가설검정 (0) | 2020.08.06 |
| 통계적 추론(구간 추정) (0) | 2020.08.04 |