2020. 8. 13. 21:27ㆍ데이터 분석 기본
아마도 데이터를 분석할 때 검증 방법론을 조금이라도 활용해보신 분은 P-value란 개념을 많이 들어보셨을 것입니다. 우리가 어떤 통계적인 검증을 수행할 때, 우리가 수립했던 가설을 채택할지 하지 않을지 결정할 때 P-value를 많이 활용합니다.
[P-value]
먼저 P-value에 대해서 정의를 하고 설명을 하는 것이 좋을 것 같습니다.
P-value(유의확률)이란 주어진 검정통계량 관측치로부터 귀무가설(H0)을 기각하게 하는 최소의 유의수준을 말합니다.
정의만 보면 상당히 난해한 것 같습니다.
우리는 앞선 포스팅에서 기각역을 정의하고 기각역안에 검정통계량이 포함되어야 귀무가설(H0)를 기각함을 알았습니다.(https://direction-f.tistory.com/30)
예를 들어 [H0: μ=x / H1: μ<x]인 귀무가설과 대립가설이 있다고 가정하겠습니다. 그렇다면 이 때 유의수준 α에 대하여 기각역 R은 아래와 같습니다.
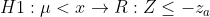
위의 기각역에서 볼 수 있는 것처럼 검정통계량 Z가 -z_a보다 작아야 우리는 H0를 기각하게됩니다. 만약 유의수준 α를 점점 키우면 어떻게 될까요? z_a값이 점점 작아짐에따라 -z_a는 커져 0에 가까워질 것입니다.(유의수준이 커짐에 따라 정규분포표에서 차지하는 영역이 커집니다.)
위에서 확인한 것과 같이 유의수준에 따라 우리는 기각여부가 달라짐을 알 수 있습니다. 그렇다면 표본으로부터 얻어진 검정 통계량(Z)를 가지고 귀무가설을 기각할 수 있게 하는 최소의 유의수준은 무엇일까요?
예를 통해 알아보겠습니다. 만약 검정통계량이 -1.96으로 구해졌다고 해보겠습니다. 만약 -z_a가 -2라면 -1.96은 기각역에 포함되지 않기때문에 H0을 기각할 수 없습니다. 즉, 적어도 -z_a가 -1.96보다 크거나 같아야 기각할 수 있게 됩니다. 자연스럽게 최소한의 기각역은 -1.96이 되고 P(Z≤-1.96)=0.025가 바로 유의확률, P-value가 됩니다.
P-value가 크다는 것은 그만큼 기각을 위한 최소한의 유의수준 α가 크다는 것이고, 이 최소한의 유의수준 α를 검증의 기준으로 삼는다면 1종 오류를 범할 위험이 크다는 것을 뜻합니다.
따라서 우리는 통계적 검증을 할 때는 0.05, 0.1과 같은 기준을 두고 P-value가 이것보다 작으면 대립가설을 채택하게 됩니다.
P-value를 구하는 식을 정리하면 다음과 같습니다.

'데이터 분석 기본' 카테고리의 다른 글
| 두 모집단의 비교(표본이 작을 때, T-Test) (0) | 2020.08.20 |
|---|---|
| 두 모집단의 비교(표본이 클 때) (0) | 2020.08.20 |
| 가설검정 > 검정통계량과 기각역 (0) | 2020.08.12 |
| 가설검정 > 가설, 검정통계량 (0) | 2020.08.09 |
| 가설검정 (0) | 2020.08.06 |