2020. 8. 6. 00:13ㆍ데이터 분석 기본
가설검정(Testing statistical hypotheses)은 모수에 대한 가설이 적합한지를 추출한 표본으로부터 판단하는 것을 나타내는 것입니다.
전국의 초등학교에서 6학년의 비만인 남자 학생(모집단)의 체중 평균이 70이고 표준편차가 7라고 가정해보겠습니다. 동시에 교육부에서 특정 다이어트 프로그램을 대대적으로 홍보했다고 가정해보겠습니다.
그럼 이러한 다이어트 프로그램 수행을 통해서 실제로 평균이 낮아졌는지를 판단하기 위해서 어떠한 과정을 거쳐야 할까요? 이러한 질문에 답을 하기 위해서 필요한 것이 가설검정입니다.
다이어트 프로그램 수행 후의 비만인 남자 학생들의 평균 몸무게를 μ라고 해보겠습니다. 우리는 전국의 비만인 남자 학생들을 다 조사할 수 없기 때문에 표본을 추출하여 표본의 평균을 구하는 것이 현실적인 방안입니다.(여기서는 임의로 49명을 추출한다고 하겠습니다.) 다만 단순히 49명의 표본평균이 모집단의 평균인 70보다 작다고 하여, 다이어트 프로그램 후의 모집단의 평균(μ)이 다이어트 프로그램 전의 모집단의 평균보다 낮아졌는지 확신하기 어렵습니다.
하지만 만약 다이어트 프로그램 전의 모집단 평균이 70이라고 할 때, 도저히 나오기 어려울 정도로 작은 값(c)이 다이어트 프로그램 후의 표본평균이라면 다이어트 프로그램이 모집단의 평균을 낮췄다고 판단할 수 있을 것입니다. 그렇다면 도저히 나오기 어려울 정도의 작은 값(c)의 기준은 어떻게 도출하게 될까요?
예를 들어 0.05의 확률을 거의 나오지 않을 정도의 확률이라고 하겠습니다. 그렇다면 아래와 같은 식을 만족하는 c값을 찾을 수 있다면, 우리는 다이어트 프로그램 후의 표본평균이 c보다 작다면 충분히 작은 값으로 판단하고 모집단의 평균을 낮춰다고 주장할 수 있을 것입니다.
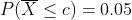
이에 답하기 위하여 우리는 표본평균의 분포를 활용해야 합니다. 모집단의 평균이 70, 표준편차가 7일 때 표본평균의 분포는 평균이 70이고 표준편차가 1(=7/√49)인 정규분포를 따르게 되고 이를 표준화하면 평균이 0이고 표준편차가 1인 표준정규분포를 따르게 됩니다.
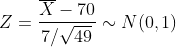
표준정규분포표를 활용하면 P(Z≤1.645)=0.05이고 우리는 이 1.645의 값을 활용하여, c값을 추정할 수 있습니다. 추정하는 식은 아래와 같이 됩니다.
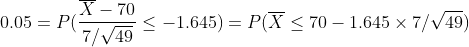
즉 c는 68.355가됩니다. 그렇기 때문에 만약 표본평균이 68.335보다 작으면 다이어트 프로그램이 효과가 있다고 주장할 수 있을 것입니다.
'데이터 분석 기본' 카테고리의 다른 글
| 가설검정 > 검정통계량과 기각역 (0) | 2020.08.12 |
|---|---|
| 가설검정 > 가설, 검정통계량 (0) | 2020.08.09 |
| 통계적 추론(구간 추정) (0) | 2020.08.04 |
| 통계적 추론(점 추정) (0) | 2020.08.03 |
| 표본평균의 분포와 중심극한 정리 (0) | 2020.07.31 |