2020. 8. 4. 21:43ㆍ데이터 분석 기본
점 추정은 모집단의 특성을 나타내는 하나의 값을 추정하는 것이었습니다. 반면 구간 추정(Interval Estimation)은 추정량(Estimator)의 분포를 활용하여 모집단의 특성을 나타내는 값을 포함하리라고 생각되는 구간을 추정하는 것입니다.
[구간 추정]
우리가 구간을 추정을 통해 모수 값(모집단의 특성을 나타내는 값)을 포함하는 구간을 추정하는데, 이 구간을 신뢰구간(Confidence Interval)이라고 부릅니다.
신뢰구간은 상한과 하한이 있고 (L,U)형태로 가지게 됩니다. 이 때 L이 -∞이고 U가 ∞라면 모수 값이 어떻게 되더라도 신뢰구간에 포함되게 될 것입니다.
따라서 우리는 상한과 하한값을 제한 할 필요가 있습니다. 이 필요로 인해서 우리가 흔히 들어본 95% 신뢰구간, 90% 신뢰구간이란 용어가 나오게 됩니다.
이와 같이 구간을 제한하게 되면 모수 값이 신뢰구간에 들어갈 확률이 100%가 아니라 95%, 90%로 제한되게 됩니다. 이 때 95%와 90%같은 수를 우리는 신뢰수준(level of confidence)이라고 부릅니다.
만약 평균이 μ이고 표준편차가 σ인 모집단이 주어졌을 때 표본평균의 분포는 평균이 μ이고 표준편차가 σ/√n을 따르게 됩니다. 우리는 이제 표본평균의 평균과 표준편차를 활용하여 표준화된 표본평균의 분포를 구할 수 있게 되고 표준화된 표본평균의 분포는 아래와 같습니다.

그렇다면 특정 값 α가 주어졌을 때(일반적으로 α값은 0.05, 0.1등으로 주어지게 됩니다.) 아래의 식을 만족하게 됩니다.
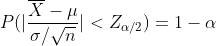
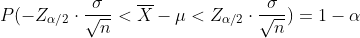

위에 식에서 확인할 수 있듯이, 모집단의 표준편차 σ가 주어지게 되면, 모집단 평균 μ에 대해서 100(1-α)% 신뢰구간은 아래와 같이 됩니다.

이때 모집단의 표준편차가 주어지지 않으면 우리는 표본자료의 표준편차를 이용하여 신뢰구간을 추정하게 됩니다.(표본자료의 표준편차는 https://direction-f.tistory.com/2를 참조하시면 됩니다.)
신뢰구간을 추정할 때 특이할 점은, 신뢰수준을 높일수록 구간이 길어진다는 것이고 표본의 크기 n이 커질수록 구간이 짧아져 모집단 평균 μ에 대해서 더 정확한 정보를 얻을 수 있다는 것입니다.
주의할 점은 95%신뢰구간이라고 한다고 하여, 모수가 95%확률 포함된다는 개념은 아닌 것입니다. 신뢰구간은 표본이 어떻게 추출되었냐에 따라 변하는 가변적인 구간입니다. 따라서 우리는 해석에 주의를 해야합니다.
따라서 신뢰구간은 동일한 방법으로(같은 크기로) 100번의 표본을 추출했을 때, 계산되는 100개의 신뢰구간 중 모평균을 포함한 신뢰구간들의 숫자가 95개 정도 된다라고 해석하면 됩니다.(출처:https://m.blog.naver.com/PostView.nhn?blogId=vnf3751&logNo=220823007712&proxyReferer=https:%2F%2Fwww.google.com%2F)
Python을 활용 신뢰구간을 추정해보도록 하겠습니다.
## 필요 Module import
import scipy.stats
from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np
## 평균 10, 표준편차 1인 정규 분포 생성 및 시각화
mu = 10
std = 1
norm_ = norm(mu,std) ## 평균 100, 표준편차 10인 정규분포 생성
## 시각화
x = np.linspace(norm_.ppf(0.01), norm_.ppf(0.99),1000) ## 1%일때 x값, 99%일때 x값 사이의 x값 생성
plt.plot(x, norm_.pdf(x),'r-', lw=2, alpha=0.6, label='norm pdf')
plt.title("population normal distribution")
plt.legend()
plt.show()
## sample 수 : 100개라 가정
data_norm = norm_.rvs(100) ## 앞에서 생성한 정규분포에서 100개 Sampling
## 표본의 통계량(estimator) 추정
mu_sample = np.mean(data_norm)
std_sample = np.std(data_norm, ddof=1)
## 상한, 하한 추정(95% 구간 z=1.96)
L_ = mu_sample - 1.96*(std_sample/np.sqrt(100))
U_ = mu_sample + 1.96*(std_sample/np.sqrt(100))
new_norm = norm(mu_sample,std_sample) ## 시각화를 위한 Sample 정보를 이용한 정규분포 생성
##시각화
plt.vlines(L_, 0, new_norm.pdf(L_), colors="g")
plt.vlines(U_, 0, new_norm.pdf(U_), colors="g")
plt.plot(x, new_norm.pdf(x),'r-', lw=2, alpha=0.6, label='norm pdf')
plt.title("sample normal distribution and confidence interval -sample: 100")
plt.legend()
plt.show()
print(L_, mu_sample, U_) ## 결과 : 9.884552789207058 10.094701914191354 10.30485103917565
## Confidence Interval을 계산하기 위한 함수 생성
mu2 = 0
std2 = 1
standard_norm = norm(mu2,std2)
def mean_confidence_interval(data, confidence=0.95):
a = np.array(data)
m, se = np.mean(a), scipy.stats.sem(a) ## 표본의 표준펀차를 활용하여 표준오차 계산
h = se * standard_norm.ppf((1+confidence)/2) ## 신뢰구간이 95%이고 α=0.05일 때, 누적확률이 97.5%인 z값 계산
return m-h,m, m+h
mean_confidence_interval(data_norm) ## 결과 (9.884556650746545, 10.094701914191354, 10.304847177636164)
##위에서 손으로 계산한 값과 일치함을 확인## sample 수 : 10000개라 가정
data_norm = norm_.rvs(1000) ## 앞에서 생성한 정규분포에서 1000개 Sampling
## 표본의 통계량(estimator) 추정
mu_sample = np.mean(data_norm)
std_sample = np.std(data_norm, ddof=1)
## 상한, 하한 추정(95% 구간 z=1.96)
L_ = mu_sample - 1.96*(std_sample/np.sqrt(1000))
U_ = mu_sample + 1.96*(std_sample/np.sqrt(1000))
new_norm = norm(mu_sample,std_sample) ## 시각화를 위한 Sample 정보를 이용한 정규분포 생성
##시각화
plt.vlines(L_, 0, new_norm.pdf(L_), colors="g")
plt.vlines(U_, 0, new_norm.pdf(U_), colors="g")
plt.plot(x, new_norm.pdf(x),'r-', lw=2, alpha=0.6, label='norm pdf')
plt.title("sample normal distribution and confidence interval -sample: 1000")
plt.legend()
plt.show()
print(L_, mu_sample, U_) ##결과 9.979423508565548 10.041601247611059 10.10377898665657
## 신뢰구간이 좁아짐을 확인
'데이터 분석 기본' 카테고리의 다른 글
| 가설검정 > 가설, 검정통계량 (0) | 2020.08.09 |
|---|---|
| 가설검정 (0) | 2020.08.06 |
| 통계적 추론(점 추정) (0) | 2020.08.03 |
| 표본평균의 분포와 중심극한 정리 (0) | 2020.07.31 |
| 정규점수, 정규확률그림 (0) | 2020.07.30 |