2021. 4. 19. 23:33ㆍ머신러닝
커널 밀도를 추정하게 되면 우리는 데이터에 대한 확률 분포를 추정한 것과 같게 됩니다. 따라서 LDA(direction-f.tistory.com/80?category=954338)에서 분포를 활용하여 Classification을 수행한 것과 동일한 원리로 Classification을 수행할 수 있게 됩니다.
즉 Bayes Rule을 적용하여 Classification을 수행하게 됩니다. Bayes Rule에 따라 아래와 같이 정리되고
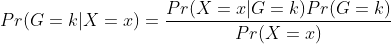
이 때 확률은 다음과 같이 정의됩니다.
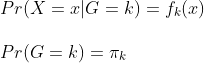
최종적으로 $Pr(G|X)$는 $Pr(X|G)$와$Pr(G=k)$에 비례하게 되므로, 최종적으로 아래와 같이 정리 됩니다.
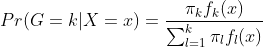
LDA와 다른 점은 우리는 $f_k(x)$를 KDE로 추정하여 활용한다는 것입니다.
Python을 활용하여 추정해보겠습니다. iris 데이터를 활용하여 추정하였습니다. 클래스나 함수를 활용하지 않고 순서대로 적어봤습니다. 기본적인 사상은 Class별로 KDE를 추정하여 Classification을 수행하는 것입니다.
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import numpy as np
from sklearn.neighbors import KernelDensity
from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
iris
X= pd.DataFrame(iris.data)
Y= pd.DataFrame(iris.target)
df = pd.concat([X,Y], axis=1)
df.columns = ["1","2","3","4","class"]
df["class"].unique()
## class 0
kde_0 = KernelDensity(bandwidth=1.0, kernel='gaussian')
kde_0.fit(df.loc[df["class"]==0].iloc[:,0:4])
logprob_0 = kde_0.score_samples(df.loc[df["class"]==0].iloc[:,0:4])
## class 1
kde_1 = KernelDensity(bandwidth=1.0, kernel='gaussian')
kde_1.fit(df.loc[df["class"]==1].iloc[:,0:4])
logprob_1 = kde_1.score_samples(df.loc[df["class"]==0].iloc[:,0:4])
## class 2
kde_2 = KernelDensity(bandwidth=1.0, kernel='gaussian')
kde_2.fit(df.loc[df["class"]==2].iloc[:,0:4])
logprob_2 = kde_2.score_samples(df.loc[df["class"]==0].iloc[:,0:4])
## priors class prob
prob_class_0 = len(df.loc[df["class"]==0])/len(df)
prob_class_1 = len(df.loc[df["class"]==1])/len(df)
prob_class_2 = len(df.loc[df["class"]==2])/len(df)
## Pr(G|sample_x)
sample_x = np.array([5,3.5,1.4,0.2]).reshape(1,-1)
sample_prob_0 =np.exp(kde_0.score_samples(sample_x))
sample_prob_1 =np.exp(kde_1.score_samples(sample_x))
sample_prob_2 =np.exp(kde_2.score_samples(sample_x))
prob_class_0_pred = prob_class_0 *sample_prob_0 /(prob_class_0 *sample_prob_0+prob_class_1 *sample_prob_1+prob_class_2 *sample_prob_2)
prob_class_1_pred = prob_class_1 *sample_prob_1 /(prob_class_0 *sample_prob_0+prob_class_1 *sample_prob_1+prob_class_2 *sample_prob_2)
prob_class_2_pred = prob_class_2 *sample_prob_2 /(prob_class_0 *sample_prob_0+prob_class_1 *sample_prob_1+prob_class_2 *sample_prob_2)
np.argmax([prob_class_0_pred,prob_class_1_pred,prob_class_2_pred])
## 0
만약 각 Feature들이 독립이라면 계산비용이 많이 소모되는 전 Feature를 활용한 KDE를 수행하지 않고 각 Feature별로 KDE를 추정하여 추정한 값들의 곱으로 확률을 나타내게 됩니다.
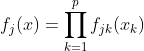
위 식에서 j는 Class를 k는 해당 feature이고 p는 전체 feature입니다. 예를 들어 Class가 3개이고 Feature가 4개이면 총 12개의 $f_jk$를 추정하게 되며 이는 Class j일때 Feature k가 나올 경향도로 이해하면 좋을 것 같습니다.
정리해본 Python 코드는 다음과 같습니다.
def kde(data, sample, class_):
result_list =[]
for j in range(4): # train data columns 수
kde = KernelDensity(bandwidth=1.0, kernel='gaussian')
kde.fit(df.loc[df["class"]==class_].iloc[:,j].values.reshape(-1,1))
result_list.append(np.exp(kde.score_samples(sample[0][j].reshape(1,-1))))
return result_list[0]*result_list[1]*result_list[2]*result_list[3]
sample_prob_0= kde(df, sample_x, 0)
sample_prob_1=kde(df, sample_x, 1)
sample_prob_2 =kde(df, sample_x, 2)
prob_class_0_pred = prob_class_0 *sample_prob_0 /(prob_class_0 *sample_prob_0+prob_class_1 *sample_prob_1+prob_class_2 *sample_prob_2)
prob_class_1_pred = prob_class_1 *sample_prob_1 /(prob_class_0 *sample_prob_0+prob_class_1 *sample_prob_1+prob_class_2 *sample_prob_2)
prob_class_2_pred = prob_class_2 *sample_prob_2 /(prob_class_0 *sample_prob_0+prob_class_1 *sample_prob_1+prob_class_2 *sample_prob_2)
np.argmax([prob_class_0_pred,prob_class_1_pred,prob_class_2_pred])
##0Sample 한 개로 비교했기 때문에 큰 의미는 없지만 간단하게 Logistic Regression을 활용한 분류기 결과도 비교해보았으며, 동일한 결과가 나왔습니다.
from sklearn.linear_model import LogisticRegression
logit = LogisticRegression(multi_class = "multinomial")
logit.fit(X, Y)
logit.predict(X)
logit.predict(sample_x) ##0
'머신러닝' 카테고리의 다른 글
| 모델 평가 및 선정 > In-Sample Prediction (0) | 2021.05.13 |
|---|---|
| 모델 평가 및 선정 > Bias, Variance (0) | 2021.05.06 |
| 커널 밀도 추정(Kernel Density Estimation, KDE) (0) | 2021.04.12 |
| KRR(Kernel Ridge Regression) (0) | 2021.03.23 |
| Kernel Regression (0) | 2021.03.23 |