2021. 2. 21. 21:29ㆍ머신러닝
LDA와 Logistic Regression같은 경우는 각 Class에 Input x가 속할 확률을 예측/추정하는 형태로 Classification이 수행됩니다.
[Linear Discriminant Analysis, LDA]
여기서 LDA는 $Pr(X|G)$를 톻한 Bayes Rule적용을 통해 X가 주어졌을 때 특정 Class에 속할확률 $Pr(G|X)$를 구하는 문제로 분류문제를 접근합니다.
LDA같은 경우는, 관측수가 적고 Input X가 정규분포를 근사할 때 효과적으로 작동하게 됩니다.
Bayes Rule적용을 통해 어떻게 사후 확률을 추론하는지를 정리해보도록 하겠습니다.

이 때 각 확률은 아래와 같이 표현하겠습니다.

최종적으로, 아래와 같이 X가 주어졌을 때 특정 Class에 속할확률 $Pr(G|X)$를 나태낼 수 있습니다.
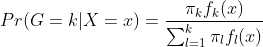
LDA를 활용하여 Classification문제를 해결하기 위해서는 $f_k(x)$에 대한 분포를 가정해야 하며, Multivariate Gaussian분포로 가정하겠습니다.

LDA는 공통 공분산을 고려하며, $\Sigma_k$ = $\Sigma$가 되어, 모든 클레스가 동일한 공분산을 가지게 됩니다.공분산 Matrix의 크기는 p*p가 됩니다.(p는 Input의 차원)
그 다음 해당 분포를 위 사후확률에 대입하여 log 변환을 취하게 되면, 아래와 같은 discriminant function을 도출할 수 있습니다.

해당 분포의 Parameter는 다음과 같이 결정 됩니다.

LDA에서도 input X에 대해 discriminant function값이 가장 높은 Class를 Input X에 대한 Class로 할당합니다.
[Quadratic Discriminant Analysis, QDA]
LDA는 Multivariate Gaussian를 추정할 때 각 Class별로 모두 공통된 공분산 Matrix를 활용한 반면, QDA는 각 Class별로 상이한 공분산 Matrix를 추정하여 활용합니다.
따라서 discriminant function은 아래와 같이 도출됩니다.

위에서 확인한 것처럼 이 결정함수는 X에 대해서 선형이 아니기 때문에 Quadaratic이라고 부르게 된것입니다.
다만, QDA는 LDA보다 추정해야할 Parameter가 더 많습니다. 따라서 작은수의 Parameter추정이 필요한 LDA가 추정 Variance가 더 적습니다. 따라서 학습해야할 관측수가 적을 때는 LDA가 효과적일때가 많습니다. 다만 공통분산에 대한 가정이 위배될 것이라 판단되는 문제에 대해서는 QDA를 적용하는 것이 더 타달할 것입니다.
이제 LDA와 QDA에 대해 실습을 해보겠습니다.
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import confusion_matrix
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
## Data Loading
iris = load_iris()
X_train = iris.data[:int(len(iris.data)*0.7)]
Y_train = iris.target[:int(len(iris.data)*0.7)]
X_test =iris.data[int(len(iris.data)*0.7):]
Y_test =iris.target[int(len(iris.data)*0.7):]
##LDA
lda = LinearDiscriminantAnalysis()
lda.fit(X_train, Y_train)
## Train Accuracy
sum(lda.predict(X_train)==Y_train)/len(Y_train) ## 1.0
## Test Accuracy & Confusion matrix
sum(lda.predict(X_test)==Y_test)/len(Y_test) ## 0.8222222222222222
confusion_matrix(Y_test,lda.predict(X_test))
## QDA
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
qda=QuadraticDiscriminantAnalysis()
qda.fit(X_train, Y_train)
## Train Accuracy
sum(qda.predict(X_train)==Y_train)/len(Y_train) ##1.0
## Test Accuracy & Confusion matrix
sum(qda.predict(X_test)==Y_test)/len(Y_test) ## 0.2222222222222222
confusion_matrix(Y_test,qda.predict(X_test))'머신러닝' 카테고리의 다른 글
| 로지스틱 회귀모형(Logistic Regression) (0) | 2021.02.23 |
|---|---|
| 선형 판별 분석(Linear Discriminant Analysis, LDA) > 차원축소 (0) | 2021.02.22 |
| 선형 분류 모형(Linear Methods for Classification) (0) | 2021.02.20 |
| Dimension Reduction Method(Principal Components Regression, Partial Least Squares) (0) | 2021.02.03 |
| Shrinkage Method2(Elastic Net, LARS) (0) | 2021.01.24 |