2020. 7. 31. 21:30ㆍ데이터 분석 기본
주어진 표본으로부터 모집단의 특성을 파악하는 것을 "추론"이라고 하며 어떻게 보면 통계학의 가장 중심이 되는 것이라고 볼 수 있습니다.
이 때, 모집단의 특성을 수치적으로 표현하는 것을 모수(Parameter)라고 합니다. 이러한 모수를 추정하기 위해서는 모집단 전체를 다 조사해야합니다. 하지만 모집단을 전부 조사하는 것은 일반적으로 어려운 일입니다.
따라서 제한된 표본으로부터 표본에서 적절한 양을 계산하여 활용하게 되는데, 이를 통계량(Statistic)이라고 부릅니다. 통계량은 표본의 관측값들에 의해 정의되는 양을 뜻합니다.
그렇다면 통계량은 모집단이 동일하더라도 표본이 바뀔때마다 바뀌는 양이 되게 됩니다. 그러므로 여러번의 표본을 뽑으면 통계량도 특정 확률분포를 갖게 됩니다. 이때 이 확률분포를 표집분포(Sampling distribution)이라고 합니다.
[표본평균의 분포]
예를 들어서 어느 모집단이 {1,2,3}으로 이루어졌으며 각 수치가 발생할 확률은 1/3으로 동일하다고 가정해보겠습니다. 그 다음 두 개의 값(X1, X2)을 복원추출하여 표본을 구성하고 해당 표본의 평균값의 분포를 추정해보겠습니다. 이 때 각 X1, X2는 집단 {1,2,3}을 가지고 각 수치가 발생할 확률이 1/3으로 모집단의 분포와 동일합니다.
모집단이 3개이고 복원추출이기 때문에 나올 수 있는 경우의 수는 3*3으로 총 9개이며, 아래와 같은 분포를 가지게 됩니다.
| 조합 | (1,1) | (1,2) | (1,3) | (2,1) | (2,2) | (2,3) | (3,1) | (3,2) | (3,3) |
| 표본평균 | 1 | 1.5 | 2 | 1.5 | 2 | 2.5 | 2 | 2.5 | 3 |
| 확률 | 1/9 | 1/9 | 1/9 | 1/9 | 1/9 | 1/9 | 1/9 | 1/9 | 1/9 |
위와 같이 우리는 표본평균의 표집분포를 구성할 수 있음을 확인 할 수 있었습니다.
마찬가지로, 평균이 μ이고 표준편차가 σ인 모집단으로부터 크기가 n인 표본(X1, X2,..,Xn)을 추출 했을 때 표본평균의 기대값과 분산도 계산될 수 있으며, 아래와 같습니다. (각 표본 값 X1, X2는 확률변수로써 모집단의 분포를 따릅니다.)
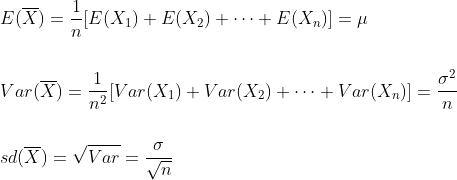
[중심극한정리]
위의 식에서 확인 할 수 있듯이, 표본평균의 분포의 평균은 모집단의 중심 μ와 일치합니다. 만약 모집단이 정규분포가 아닌경우 표본평균의 분포는 모집단의 분포에 따라 다르게 나타나기도 합니다. 하지만, 표본의 크기 n이 큰 경우에는 표본평균의 분포는 모집단의 분포와 무관하게 근사적으로 정규분포를 따르게 됩니다. 이것이 중심극한정리입니다.
다시 정리하면
모집단의 평균이 μ이고 표준편차가 σ일 때, 임의로 추출한 표본의 표본평균은 표본의 크기 n이 충분히 클 때 (통상 적으로 30 이상) 근사적으로 정규분포를 따르게 되며, 그 때 평균은 μ이고 분산은 σ/√n이 됩니다. 이를 표준화 하여 나타내면 아래와 같이 표현됩니다.
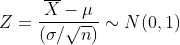
'데이터 분석 기본' 카테고리의 다른 글
| 통계적 추론(구간 추정) (0) | 2020.08.04 |
|---|---|
| 통계적 추론(점 추정) (0) | 2020.08.03 |
| 정규점수, 정규확률그림 (0) | 2020.07.30 |
| 연속확률분포, 정규분포, 표준정규분포 (0) | 2020.07.26 |
| 포아송 분포 (0) | 2020.07.23 |