2020. 7. 14. 22:45ㆍ데이터 분석 기본
두 개 이상의 사건이 있을 때 한 사건이 다른 사건의 확률에 영향을 미치는 경우를 본 적이 있으실 겁니다. 예를 들어 성인 남성과 남자 아동이 함께 있는 집단에서 임의로 한 사람을 뽑았을 때 그 사람이 성인 남성인 사건을 A라고 키가 180cm 이상일 사건을 B라고 해보겠습니다.
그렇다면 전체 집단에서 임의적으로 특정 인원을 뽑았을 때 성인 남성일 확률과 키가 180cm이상인 사람이 뽑혔을 때 성인 남성일 확률이 상이할 것이라는 것을 우리는 직관적으로 알 수 있습니다.
[조건부 확률]
위의 예와 같이 사건 B와 관련된 정보가 우선적으로(사전적으로) 주어졌을 때 사건 A의 변화된 확률을 "B가 주어졌을 때 사건 A의 조건부 확률"이라고 하며 P(A|B)로 표기 합니다. 조건부 확률을 계산하는 공식은 아래와 같습니다.
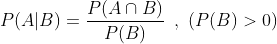
위의 조건부 확률의 정의를 이용하면, 아래와 같은 식을 유도할 수 있습니다.

만약 이 때 사건 A와 B의 교집합일 확률이 사건 A일 확률 P(A)와 사건 B일 확률 P(B)의 곱으로 표현된다면, 사건 A와 사건 B를 서로 독립이라고 할 수 있습니다.

만약 사건 A와 사건 B가 독립이라면 조건부 확률을 아래와 같이 표현됩니다.

[베이즈 정리]
우리는 표본 공간이 교집합이 없는 사건(배반사건)들의 모임으로 구성될 수 있음을 알 수 있습니다.
예를 들어 직장인들을 "20대 미만", "20대 이상 30대 미만", "30대 이상"으로 교집합 없이 구성 할 수 있을 것입니다.
이와 같이 각 사건들이 배반사건들이면서 사건들의 합집합이 표본공간을 구성할 때, 이 때 각 사건을 표본공간의 분할이라고 부릅니다.
우리는 위에서 직장인을 "20대 미만", "20대 이상 30대 미만", "30대 이상"으로 구분했습니다. 이 사건들을 각각 A1, A2, A3라고 하겠습니다. 추가적으로 직장인들 중에서 담배를 피는 사건을 B라고 하겠습니다. A1, A2, A3는 교집합이 없기 때문에 직장인들 중 담배를 피는 사건은 아래와 같이 표현할 수 있습니다.

그렇다면 직장인들 중 담배를 필 확률은 아래와 같이 계산될 수 있습니다.

위와 같은 계산을 일반화 한 것이 총확률의 법칙이며, 아래와 같이 정의 됩니다.

그렇다면 이제 우리가 지금까지 정리했던 조건부 확률에서 교집합을 정의한 식과 총확률의 법칙에서 정의된 식을 활용하여 베이즈정리를 아래와 같이 정의할 수 있습니다.

파이썬을 활용해서 공식을 통해 도출한 값과 실제로 손으로 푸는 값이 같은 결과를 보는지 확인해 보았습니다.
import pandas as pd
## 가상 데이터 생성
smoking_group = {"ten":{"non":10, "smoking" :0},
"twenty":{"non":5, "smoking" :5},
"thirty":{"non":2, "smoking" :8}}
table = pd.DataFrame(smoking_group).transpose()
## 각각 확률 계산
P_ten = table.loc["ten"].sum()/table.values.sum()
P_twenty = table.loc["twenty"].sum()/table.values.sum()
P_thirty= table.loc["thirty"].sum()/table.values.sum()
P_smoking = table["smoking"].sum()/table.values.sum()
P_smoking_given_ten = table.loc["ten"]["smoking"]/table.loc["ten"].sum()
P_smoking_given_twenty = table.loc["twenty"]["smoking"]/table.loc["twenty"].sum()
P_smoking_given_thirty = table.loc["thirty"]["smoking"]/table.loc["thirty"].sum()
P_twenty_given_smoking = P_twenty*P_smoking_given_twenty/((P_ten*P_smoking_given_ten)+(P_twenty*P_smoking_given_twenty)+(P_thirty*P_smoking_given_thirty))
print("P_twenty_given_smoking:{}".format(round(P_twenty_given_smoking,3))) ##0.385
print("담배피는 사람일 때 20대일 확률:{}".format(round(5/13,3))) ##0.385
'데이터 분석 기본' 카테고리의 다른 글
| 확률분포의 기댓값(평균), 표준편차 (0) | 2020.07.19 |
|---|---|
| 확률변수, 확률분포 (0) | 2020.07.16 |
| 확률의 기본 연산 (0) | 2020.07.12 |
| 확률의 이해 (0) | 2020.07.11 |
| 산점도, 공분산, 상관계수 (0) | 2020.07.09 |