2021. 3. 9. 19:19ㆍ머신러닝
Natural Cubic Spline을 다루기에 앞서, 지난 포스팅(direction-f.tistory.com/85)에 다루었던 Regression Spline에 대해서 다시 한 번 정리하고 가보도록 하겠습니다.
Regression Spline은 절단점에서 연속이라는 제한조건을 추가로 부여하여 다항식을 적합하는 것입니다. 이는 Basis Exapansion관점에서 해당 제한조건을 만족하는 적절한 Basis Function을 찾아서 Fitting 하는 것과 마찬가지 였습니다.
마찬가지로 Basis Exapansion 관점에서 추가적인 제한조건을 추가하게 되면 기존과 다른 Basis function을 찾게 될 것임을 직관적으로 예상할 수 있습니다. 여기서 가장 작은 절단점보다 값이 작은 구역과 가장 큰 절단점보다 값이 큰 구역에서 Cubic이 아니라 선형으로 적합하라는 제한조건을 추가하면 Natural Cubic Spline이 됩니다.
Python에서 Regression Cubic Spline과 Natural Cubic Spline을 적합해보도록 하겠습니다. 지난 포스팅(direction-f.tistory.com/85)에서는 Regression Cubic Spline을 적합하기 위해 활용할 Basis Function을 먼저 정의했지만 여기서는 bs function을 이용하여 자동으로 적합하도록 하겠습니다. 즉 bs function은 Regression Cubic Spline을 적합하는 것이고 cr function은 Natural Cubic Spline을 적합하기 위해 활용하는 함수입니다.
데이터는 이전 포스팅에서 다루었던 것과 동일하게 Wage 데이터를 쓸것이며, 기본적인 import하는 package는 이전 포스팅을 참조하면 좋을 것 같습니다.
from patsy import dmatrix
import statsmodels.api as sm
import statsmodels.formula.api as smf
data = pd.read_csv("Wage.csv")
## bs function - Cubic Spline
## bs function - Cubic Spline
pred1 = fit1.predict(dmatrix("bs(valid, knots=(38,59), include_intercept=False)", {"valid": valid_x}, return_type='dataframe'))
transformed_x = dmatrix("bs(train, knots=(38,59), degree=3, include_intercept=False)", {"train": train_x},return_type='dataframe')
fit1 = sm.GLM(train_y, transformed_x).fit()
xp = np.linspace(valid_x.min(),valid_x.max(),70)
pred1 = fit1.predict(dmatrix("bs(xp, knots=(38,59), include_intercept=False)", {"xp": xp}, return_type='dataframe'))
## 시각화
plt.scatter(data.age, data.wage, facecolor='None', edgecolor='k', alpha=0.1)
plt.plot(xp, pred1, label='Specifying degree =3 with 3 knots')
plt.show()
## Basis Function(##length(knots)(2) + degree(3) -> 5 basis functions)
plt.scatter(train_x, transformed_x.iloc[:,1])
plt.scatter(train_x, transformed_x.iloc[:,2])
plt.scatter(train_x, transformed_x.iloc[:,3])
plt.scatter(train_x, transformed_x.iloc[:,4])
plt.scatter(train_x, transformed_x.iloc[:,5])

## natural spline
transformed_x_cr = dmatrix("cr(train,knots=(38,59))", {"train": train_x},return_type='dataframe')
fit_cr = sm.GLM(train_y, transformed_x_cr).fit()
xp = np.linspace(valid_x.min(),valid_x.max(),70)
pred_cr = fit_cr.predict(dmatrix("cr(xp, knots=(38,59))", {"xp": xp}, return_type='dataframe'))
## 시각화
plt.scatter(data.age, data.wage, facecolor='None', edgecolor='k', alpha=0.1)
plt.plot(xp, pred1, label='bs')
plt.plot(xp, pred_cr, color = 'red', label = "cr")
plt.show()
##length(knots)(2) + 2 - > 4 basis functions
plt.scatter(train_x, transformed_x.iloc[:,1])
plt.scatter(train_x, transformed_x.iloc[:,2])
plt.scatter(train_x, transformed_x.iloc[:,3])
plt.scatter(train_x, transformed_x.iloc[:,4])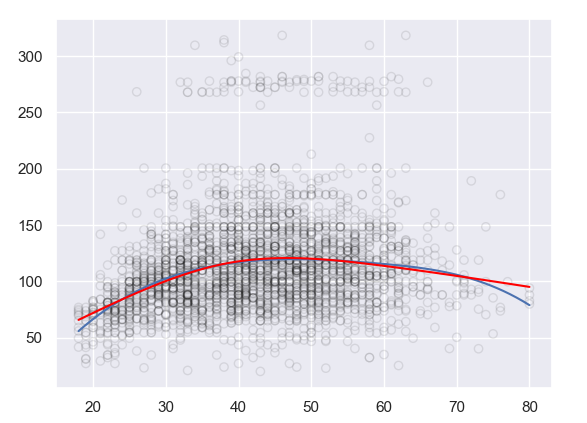

Natural Spline의 경우 제한조건이 추가되었기 때문에, 자유도가 더 낮고 추정하는 Basis funciton의 수가 줄어들게 됩니다.
'머신러닝' 카테고리의 다른 글
| Kernel Regression (0) | 2021.03.23 |
|---|---|
| Smoothing Spline (0) | 2021.03.12 |
| Piecewise Polynomial and Regression Splines (3) | 2021.03.02 |
| 로지스틱 회귀모형(Logistic Regression) (0) | 2021.02.23 |
| 선형 판별 분석(Linear Discriminant Analysis, LDA) > 차원축소 (0) | 2021.02.22 |