2021. 3. 2. 23:22ㆍ머신러닝
지금까지 우리는 input feature X에 대한 선형 모형을 주로 다루었습니다. 이번 포스팅에서는 input feature에 추가적인 항을 붙이거나, 입력 변수 X를 transformation을 함으로써 비선형성을 부여하는 방법에 대해서 다루고자 합니다.
가장 간단한 비선형성 부여 방법은 X의 다항식들을 추가 input으로 활용하는 것입니다. 예를 들어 X에 추가적으로 $X^2$, $X^3$과 같은 항을 활용하는 것입니다. 더 나아간다면 구간 별로 다른 다항식을 활용하는 방법도 있을 것입니다.
이번 포스팅에서는 이러한 방법들 중에서 크게 1) Polynomial Regession 2) Piecewise Polynomial Regession 3) Regression Spline(cubic/natural cubic)에 대해서 정리하도록 하겠습니다.
데이터 Introudction Statistical learning에 나온 Wage 데이터를 활용하고자 하며, 데이터 및 파이썬 코드는 아래 블로그 3개를 참조하였습니다. 첫 번째 블로그에서 데이터를 다운로드 할 수 있습니다.
www.analyticsvidhya.com/blog/2018/03/introduction-regression-splines-python-codes/
www.kaggle.com/renanhuanca/regression-splines
towardsdatascience.com/non-linear-regression-basis-expansion-polynomials-splines-2d7adb2cc226
[Polynomial Regession]
종속변수와 입력변수 X와의 관계가 선형이 아닌 경우, 단순 선형회귀 모형을 적합했을 때 정상적으로 적합되지 않을 수 있습니다.
이럴 때 아래와 같이 입력변수를 다항식으로 확장하여 Fitting을 하여 이러한 한계점을 극복할 수 있습니다.

Polynomial Regession은 Python의 numpy를 활용하면 간단하게 구현할 수 있습니다.
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from patsy import dmatrix
import statsmodels.api as sm
import statsmodels.formula.api as smf
# read data_set
data = pd.read_csv("Wage.csv")
data.head()
data_x = data["age"]
data_y =data["wage"]
train_x, valid_x, train_y, valid_y = train_test_split(data_x, data_y, test_size=0.33, random_state=7)
##### Polynomial regression
weights = np.polyfit(train_x, train_y, 2) ## degree = 2
print(weights)
poly_model = np.poly1d(weights)
pred = poly_model(valid_x)
xp = np.linspace(valid_x.min(),valid_x.max(),70)
pred_plot = poly_model(xp)
plt.scatter(valid_x, valid_y, facecolor='None', edgecolor='k', alpha=0.3)
plt.plot(xp, pred_plot, linewidth=3)
plt.show()
[Piecewise Polynomial]
특정 구간별로 Polynomial을 적합하는 것을 Piecewise polynomial이라고 합니다. 예를 들어 Input 변수의 범위가 30~80이라고 했을 때, 50미만 구간에서 그리고 50이상 구간에서 서로 다른 다항식을 fitting한 것입니다.
예시적으로, 아래 수식은 두 개의 구간이 주어졌다고 했을 때 3차 다항식을 각 구간별로 fitting한 것을 나타냅니다. 즉 구간이 2개이기 때문에 2개의 다항식을 Fitting합니다.
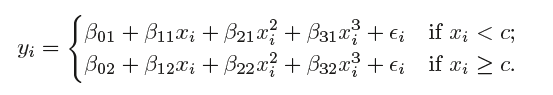
#### Piecewise Polynomial
## 구간 나누기
knot_bin = (train_x.max()-train_x.min())/3
knot_1 = int(train_x.min()+knot_bin)
knot_2 = int(train_x.min()+knot_bin+knot_bin)
def split_(row):
if row <= knot_1:
return "knot1"
elif row > knot_1 and row <= knot_2:
return "knot2"
else:
return "knot3"
region_ = train_x.apply(lambda x:split_(x))
## 지역별로 0차 함수 적합(Constant)
df_steps = pd.concat([train_x, region_, train_y], keys =['age','region','wage'], axis=1)
df_steps_dummies = pd.get_dummies(df_steps["region"])
fit3 = sm.GLM(df_steps.wage, df_steps_dummies).fit()
## 시각화
df_steps["xp"] = np.linspace(train_x.min(),train_x.max()-1,len(df_steps))
df_steps["new_region"] = df_steps.apply(lambda x:split_(x["xp"]),axis = 1)
df_steps_dummies_xp = pd.get_dummies(df_steps["new_region"])
df_steps["pred"] = fit3.predict(df_steps_dummies_xp)
plt.scatter(train_x, train_y, facecolor='None', edgecolor='k', alpha=0.3)
plt.plot(df_steps.loc[df_steps["new_region"]=="knot1"]["xp"], df_steps.loc[df_steps["new_region"]=="knot1"]["pred"], linewidth=2, color = 'r')
plt.plot(df_steps.loc[df_steps["new_region"]=="knot2"]["xp"], df_steps.loc[df_steps["new_region"]=="knot2"]["pred"], linewidth=2, color = 'g')
plt.plot(df_steps.loc[df_steps["new_region"]=="knot3"]["xp"], df_steps.loc[df_steps["new_region"]=="knot3"]["pred"], linewidth=2, color = 'b')
plt.show()

만약 위에 Code에서 1차 선형식으로 적합하고 싶다면 아래와 같이 Code를 활용하면 됩니다.
## 지역별 1차 함수 적합
model_poly_r_1 = sm.GLM(df_steps.loc[df_steps["new_region"]=="knot1"]["wage"],df_steps.loc[df_steps["new_region"]=="knot1"]["age"]).fit()
model_poly_r_2 = sm.GLM(df_steps.loc[df_steps["new_region"]=="knot2"]["wage"],df_steps.loc[df_steps["new_region"]=="knot2"]["age"]).fit()
model_poly_r_3 = sm.GLM(df_steps.loc[df_steps["new_region"]=="knot3"]["wage"],df_steps.loc[df_steps["new_region"]=="knot3"]["age"]).fit()
pred_r_1 = model_poly_r_1.predict(df_steps.loc[df_steps["new_region"]=="knot1"]["xp"])
pred_r_2 = model_poly_r_2.predict(df_steps.loc[df_steps["new_region"]=="knot2"]["xp"])
pred_r_3 = model_poly_r_3.predict(df_steps.loc[df_steps["new_region"]=="knot3"]["xp"])
plt.scatter(train_x, train_y, facecolor='None', edgecolor='k', alpha=0.3)
plt.plot(df_steps.loc[df_steps["new_region"]=="knot1"]["xp"], pred_r_1 , linewidth=2, color = 'r')
plt.plot(df_steps.loc[df_steps["new_region"]=="knot2"]["xp"], pred_r_2 , linewidth=2, color = 'g')
plt.plot(df_steps.loc[df_steps["new_region"]=="knot3"]["xp"], pred_r_3 , linewidth=2, color = 'b')
plt.show()
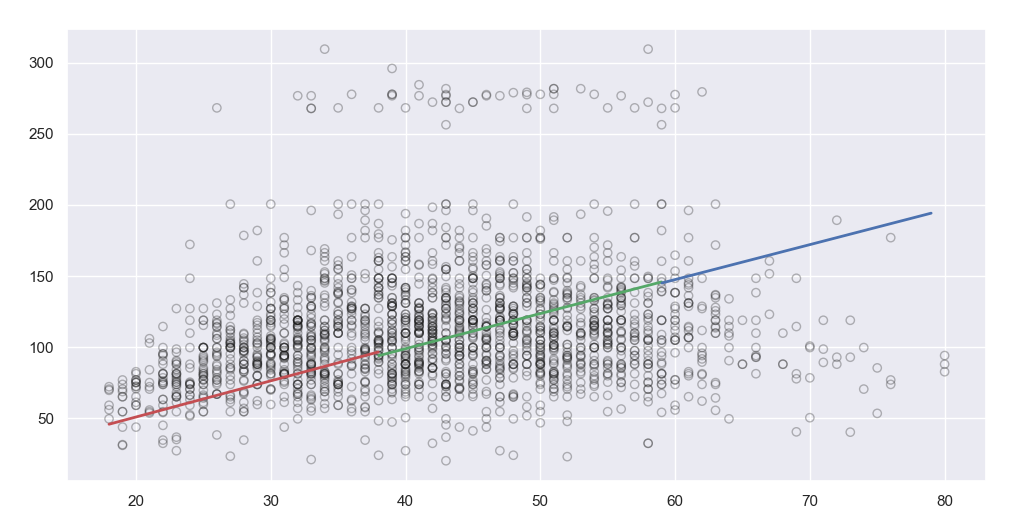
[Regression Spline]
Piecewise polynomial의 경우 knot이라고 불리는 절단점에서 Continuous하지 않음을 확인할 수 있습니다. Regression Spline은 절단점에서 연속이라는 제한조건을 추가로 부여하여 다항식을 적합하는 것입니다.
Regression Spline을 설명하기에 앞서 Basis Expansion이란 개념에 대해서 간략히 정리하도록 하겠습니다. Basis Expansion이란 Input feature X를 그대로 모델 적합을 위해 활용하지 않고 입력변수 X를 변환한 후 모델 적합을 하는데 활용하는 것입니다.

여기서 $h_m(X)$는 Basis function으로 X를 변환해주는 역할을 합니다. 위에서 살펴 본 3차 Polynomial Regression 에서 $X^2$, $X^3$이 일종에 Basis function으로 볼 수 있습니다.
이제 절단점에서 연속이라는 제한조건을 만족하는 Basis function을 찾는것이 중요한데,
3차 다항식 같은 경우, 아래와 같은 truncated power basis function을 각 절단점 마다 추가함으로써, 제한조건을 만족하는 Basis function을 만들어낼 수 있습니다.

2개의 절단점을 가지고 있다고 한다면 3차 다항식의 Regression Spline의 basis function은 아래와 같이 표현됩니다.

즉 기존에 활용했던 1, $X$, $X^2$, $X^3$에 truncated power basis function를 추가한 것입니다.
Python에서 직접 Basis function으로 X를 transformation 시킨 후 regression을 수행해보도록 하겠습니다.
## Cubic Spline - 직접 Basis function 생성 및 활용
knot_bin = (train_x.max()-train_x.min())/3
knot_1 = int(train_x.min()+knot_bin)
knot_2 = int(train_x.min()+knot_bin+knot_bin)
h1 = np.ones_like(train_x)
h2 = np.copy(train_x)
h3 = h2 ** 2
h4 = h2 ** 3
h5 = np.where(train_x < knot_1, 0, (train_x - knot_1) ** 3)
h6 = np.where(train_x < knot_2, 0, (train_x - knot_2) ** 3)
df_reg_spline = pd.DataFrame([h1,h2,h3,h4,h5,h6]).T
df_reg_spline.columns = ["h1","h2","h3","h4","h5","h6"]
model_reg_spline = sm.GLM(train_y, df_reg_spline.values).fit()
## 시각화
xp = np.linspace(valid_x.min(),valid_x.max(),70)
v_h1 = np.ones_like(xp)
v_h2 = np.copy(xp)
v_h3 = v_h2 ** 2
v_h4 = v_h2 ** 3
v_h5 = np.where(xp < knot_1, 0, (xp - knot_1) ** 3)
v_h6 = np.where(xp < knot_2, 0, (xp - knot_2) ** 3)
V_H = np.vstack((v_h1,v_h2,v_h3,v_h4,v_h5,v_h6)).T
pred_plot = model_reg_spline.predict(V_H)
plt.scatter(train_x, train_y, facecolor='None', edgecolor='k', alpha=0.3)
plt.plot(xp, pred_plot, linewidth=3, color='red', alpha = 0.7)
plt.show()
그림에서 보는 것과 같이 각 절단점에서도 끊어지지 않고 연속적으로 나옴을 확인할 수 있습니다.
** Regression Spline에서 절단점(K)가 더 많아지고, Basis function으로 활용하는 함수의 차수(M)가 높아지면 일반적으로 아래와 같이 Basis funciton을 만들어 낼 수 있습니다.

'머신러닝' 카테고리의 다른 글
| Smoothing Spline (0) | 2021.03.12 |
|---|---|
| Natural Cubic Spline (0) | 2021.03.09 |
| 로지스틱 회귀모형(Logistic Regression) (0) | 2021.02.23 |
| 선형 판별 분석(Linear Discriminant Analysis, LDA) > 차원축소 (0) | 2021.02.22 |
| 선형 판별 분석(Linear Discriminant Analysis, LDA) (0) | 2021.02.21 |