2021. 3. 23. 00:00ㆍ머신러닝
Kernel Regression이라고 불리는 것 중에는 크게 2가지 방안이 있습니다. 첫번째는 Non-parametric한 방법으로 어떠한 함수의 형태를 Fix하지 않고 Kernel을 Weight으로써 활용하여 방안입니다.
두번째는 Kernel trick Regression이라고 하여, Input X를 Kernel함수를 통하여 특정값에 Mapping하여 해당 Mapping된 Value들을 활용하여 OLS추정법을 활용하여 target Y를 예측하는 것입니다. Python의 sklearn은 Kernel Ridge Regression(KRR) method를 제공하는데 두 번째 방안과 같이 작동을 하게 됩니다.
먼저 Non-parametric 방안에 대해서 정리해보도록 하겠습니다.
[Kernel Regression(Non-parametric)]
Non-parametric Kernel Regression은 Kernel 함수의 값을 Weight으로써 활용하는데, 가중평균을 생각해보면 직관적으로 이해할 수 있을 것입니다. 쉽게말하면 나와 가까이 있는 애들에게 더 가중치를 준다는 것이고, 더 가까이 있는 정도를 Kernel 함수를 통해서 계산을 한다는 것입니다.
예를 들어 아래와 같이 데이터가 있다고 가정해보겠습니다.
| X | Y |
| 1 | 10 |
| 2 | 20 |
| 3 | 30 |
| 4 | 40 |
| 5 | 50 |
| 6 | 60 |
만약 우리가 X가 1.5일 때의 Y 값을 구한다면 가장 간단한 방법으로 X=1.5와 가장 가까운 값 X=1일때와 X=2일때의 Y값의 평균을 구하는 것입니다. 그렇다면 X=1.5일 때 Y값으로 우리는 15((10+20)/2)라고 추정해볼 수 있을 것입니다.(가중치로 표현한다면 근처 값에만 가중치를 0.5씩 주고, 나머지 값들에는 가중치를 0으로 준것과 같습니다.)
즉 Y값을 구하고 싶을 때의 가중평균의 계산식을 아래와 같습니다.
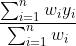
이와 같이 근처에 있는 값에 가중치를 두어 계산을 하는 것이 Non-parametric Kernel regression의 주요 사상이며, Kernel값을 비중으로 활용해주면 됩니다. 따라서 Kernel 함수를 활용하여 예측값을 표현하면 아래와 같습니다.

정말 많은 Kernel함수들이 있지만, 가까울 수록 함수값이 커지는 주요 Kernel 함수로는 Gaussian Kernel이 있고 아래와 같습니다.
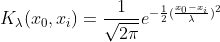
Python에서 Statsmodel에서 Non-parametric Kerner regression을 위한 Method를 제공해주고 있습니다. 별도로 Class를 구성하여 계산을 해보고 Statsmodels결과 값과 비교해보도록 하겠습니다.
from scipy.stats import norm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
## Class 구성
class Kernel_regression:
def __init__(self, x,y,width):
self.x = x
self.y = y
self.width = width
## Gaussian 커널
def gaussian_kernel(self,z_1,z_2):
return (1/math.sqrt(2*math.pi))*np.exp(-0.5*np.sum(((z_1-z_2)/self.width)**2))
def predict(self,X,ker):
kernels = []
if ker == "gaussian":
for xi_2 in X:
for xi in self.x:
kernels.append(self.gaussian_kernel(xi, xi_2)) ##새로운 input X에 대한 Kernel 함수값 계산
kernels = np.array(kernels).reshape(len(X),-1)
results =[]
for kernel in kernels:
results.append(np.sum(kernel* self.y)/np.sum(kernel))
return results
gkr = Kernel_regression([10,20,30,40,50,60,70,80,90,100,110,120], [2337,2750,2301,2500,1700,2100,1100,1750,1000,1642, 2000,1932], 10)
gkr.predict([50], "gaussian") ## [1995.2858171576065]
## Statsmodel 패키지
from statsmodels import nonparametric
x= [10,20,30,40,50,60,70,80,90,100,110,120]
y = [2337,2750,2301,2500,1700,2100,1100,1750,1000,1642, 2000,1932]
kreg = nonparametric.kernel_regression.KernelReg(endog = y, exog = x, var_type='c', ckertype='gaussian',reg_type = "lc", bw ="10").fit([50,60])
kreg[0] ## array([1974.12925314])위 두 값을 활용하면 거의 동일한 결과가 나옴을 확인할 수 있습니다. 지금까지 다루었던 Kernel Regression 방안은 Nadaraya-Watson kernel regression라고 불리는 방법입니다.
Nadaraya-Watson kernel regression은 한가지 단점을 가지고 있는데 위의 Python Code에서 Input X는 10으로 시작하는데, 10보다 작은 데이터가 없기 때문에 가중치의 불균형을 일으키게 됩니다. 따라서 이를 극복하기 위한 방안이 제시되었습니다.
그 방안으로느 Non-parametric Kernel Regression의 일환으로 Kernel기반에 Local Linear Regression을 활용하는 방안입니다. 이 것은 Input 변수 각 한 Point $x_0$에 대해서 추정한 Kernel값을 활용한 Linear Regression을 수행하는 것입니다. 따라서 각 Point마다 Weighted Regression을 수행하게 됩니다.
Weighted Regression 수행하기 위한 최적화 식은 아래와 같습니다.

이 때 추정값은 아래와 같습니다.

식에서 확인할 수 있듯이 각 포인트마다 추정하는 Parameter가 상이하게 됩니다.
Python Code는 Statsmodel 패키지를 활용하면 간단하며, reg_type을 "ll"로 설정하면 됩니다. "lc"로 설정하게 되면 Nadaraya-Watson kernel regression이 됩니다.
kreg = nonparametric.kernel_regression.KernelReg(endog = y, exog = x, var_type='c', ckertype='gaussian',reg_type = "ll", bw ="10").fit([50])
kreg[0] ## array([2017.10929616])
## 비교
kreg_lc=[]
kreg_ll=[]
for i in range(0,120):
kreg_lc.append(nonparametric.kernel_regression.KernelReg(endog = y, exog = x, var_type='c', ckertype='gaussian',reg_type = "lc", bw ="10").fit([i])[0][0])
kreg_ll.append(nonparametric.kernel_regression.KernelReg(endog = y, exog = x, var_type='c', ckertype='gaussian',reg_type = "ll", bw ="10").fit([i])[0][0])
plt.plot(x,y)
plt.plot(range(0,120), kreg_lc, color = "red", label= "lc")
plt.plot(range(0,120), kreg_ll, color = "green", label = "ll")
plt.legend()
plt.show()
Reference:
Kernel Regression from Scratch | Kunj Mehta | Towards Data Science
The Elements of Statistical Learning
www.apimirror.com/statsmodels/generated/statsmodels.nonparametric.kernel_regression.kernelreg
'머신러닝' 카테고리의 다른 글
| 커널 밀도 추정(Kernel Density Estimation, KDE) (0) | 2021.04.12 |
|---|---|
| KRR(Kernel Ridge Regression) (0) | 2021.03.23 |
| Smoothing Spline (0) | 2021.03.12 |
| Natural Cubic Spline (0) | 2021.03.09 |
| Piecewise Polynomial and Regression Splines (3) | 2021.03.02 |