2021. 5. 30. 22:51ㆍ머신러닝
이번 포스팅에서는 앞의 포스팅에서 언급했던 모델 Selection 방안에 대해 이어서 정리하도록 하겠습니다. 결국 올바른 모델을 선정 한다는것은 over-fitting도 under-fitting도 되지 않고 새로운 데이터에 대해서 오차가 적도록 작동하는 모델을 찾는 것입니다.
이번 포스팅에서는 $C_p$, BIC, SRM(VC-dimension)에 대해서 간략히 정리하도록 하겠습니다.(AIC: https://direction-f.tistory.com/93)
[$C_p$ statistic]
먼저 $C_p$ statistic은 멜로우즈 $C_p$(Malloiws $C_p$)라고 불리는 값입니다. $C_p$는 아래와 같이 정의 됩니다.

p는 활용한 변수 의 수, n은 관측값의 개수, $RSS_p$는 p개의 변수를 활용했을 때 Residual sum of squares이고 $\S^2$은 활용할 수 있는 전체 변수를 활용했을 때의 잔차평균제곱(residual mean square) 입니다.
OLS에서 $C_p$ statistic에 포함되어 있는 RSS를 아래와 같이 표현할 수 있습니다.

이때 $\beta$는 true 값입니다. 따라서 실제로 우리가 추정한 파라미터가 True값과 가까워 질 수록 $C_p$값은 p에 가까워집니다.(http://rafalab.github.io/pages/754/section-09.pdf)
결과적으로 일반적으로 $C_p$값이 p에 가까울 수록 좋은 모형입니다. 즉 $C_p$값과 할용한 변수 개수 p 값의 차이가 적은 모형을 선택합니다.
[BIC]
BIC는 AIC와 거의 유사한 형태로 정의됩니다.

BIC는 변수가 늘어남에 따른 Penalty가 좀 더 큽니다. 따라서 변수가 큰 것에 대해 민감한 경우라면 BIC를 참고하는 것이 나을 수 있습니다.
AIC와 마찬가지로 BIC도 낮을 수록 모델이 더 적합함을 나타냅니다.
BIC는 Bayesian information criterion의 약자로, 말그대로 Bayesian approach를 적용하여 도출된 값입니다. BIC는 모델M이 주어졌을 때 데이터가 x일 확률을 최대로 하는 것을 찾는겂이니다. 즉 P(x|M)을 표현하는 것인데, 아래와 같이 정의됩니다.(https://en.wikipedia.org/wiki/Bayesian_information_criterion)
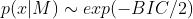
보는것과 같이 BIC가 작을 수록 모델이 주어졌을 때 x가 나올 확률이 높아집니다.
[SRM, Structural risk minimization]
SRM도 마찬가지로 모델 복잡도를 높힘으로써 발생하는 Overfitting을 막는 역할을 하게 됩니다. SRM을 설명하기 전에 VC dimension(Vanpik-Chervonenkis dimension)에 대해서 정리하면 VC 차원은 Sample을 모두 분류할 수 있는 경우의 수라고 할 수 있습니다. 일반적으로 선형 binary classifier의 경우 VC dimension은 변수의 차원이 n이라고 가정했을 때 n+1이 됩니다. 우리는 VC dimension이 높아질수록 모델 복잡도가 늘어남을 알 수 있습니다.
VC dimension을 활용한 Test error의 Upper bound를 구할 수 있는데 아래와 같습니다.
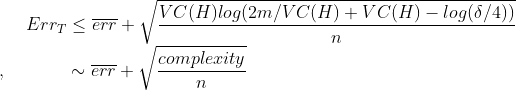
위의 식에서 보는 것과 같이 training set error가 커질수록(모델복잡도가 작을수록 일반적으로 커짐) 그리고 모델 복잡도가 커질수록 Upper bound가 커지게 됩니다. SRM은 Test error의 Upper bound가 가장 작은 것을 선택합니다.
'머신러닝' 카테고리의 다른 글
| 모델 평가 및 선정 > Bootstrap Method (0) | 2021.06.28 |
|---|---|
| 모델 평가 및 선정 > Cross-Validation (0) | 2021.06.10 |
| 모델 평가 및 선정 > In-Sample Prediction (0) | 2021.05.13 |
| 모델 평가 및 선정 > Bias, Variance (0) | 2021.05.06 |
| 커널 밀도 추정 기반 Classification (0) | 2021.04.19 |