2020. 11. 1. 22:45ㆍ계량경제학
이번 포스팅에서는 Binary(0 or 1 값을 가지는) 종속변수를 예측 및 추정할 때 사용하는 회귀분석을 정리해보도록 하겠습니다. 종속변수가 Binary일 때 주로 로짓(Logit) 회귀모형과 프로빗(Probit)회귀모형을 많이 활용합니다.
아래와 같은 선형 회귀모형이 있다고 해보겠습니다.
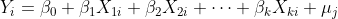
종속변수 $Y_i$가 binary변수 일 때 위 선형 모형은 선형 확률 모형(Linear probability model)로 아래와 같이 표현될 수 있습니다.
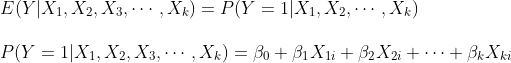
여기서 계수 $\beta_j$는 다른 $X$값들이 변화하지 않을 때, $Y_i=1$일 확률의 변화로 해석될 수 있습니다. $\beta_j$는 다른 회귀분석과 마찬가지로 OLS를 활용하여 추정될 수 있습니다.
HMDA 데이터를 활용하여, 선형 확률 모형을 Fitting 해보겠습니다. HMDA데이터는 R에서 AER 라이브러리를 활용하여 다운 받았습니다. 위 데이터에서 deny가 1이면 mortage 신청이 거부 된 것이고, deny=0이면 mortage 신청이 승인된 것입니다.
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import seaborn as sns
# Data loading
HMDA = pd.read_csv("HMDA.csv")
HMDA.head()
HMDA.info()
HMDA["deny_binary"]=HMDA["deny"].apply(lambda x : 1 if x=="yes" else 0)
## deny mod1
denymod1 = smf.ols("deny_binary~pirat", data = HMDA).fit()
denymod1.summary()
'''
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.0799 0.021 -3.777 0.000 -0.121 -0.038
pirat 0.6035 0.061 9.920 0.000 0.484 0.723
==============================================================================
'''
## 시각화
HMDA["linear"]= denymod1.predict(HMDA["pirat"])
plt.plot(HMDA["pirat"],HMDA["deny_binary"] ,"o")
plt.xlim(-0.2, 3.2)
plt.ylim(-0.5,1.5)
plt.xlabel("pirat")
plt.ylabel("deny")
sns.lineplot(data=HMDA, x="pirat", y="linear")
plt.show()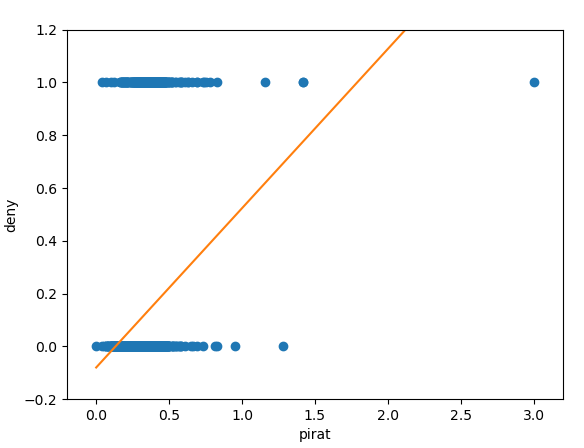
선형 확률 모형은 위 그림에서 본것과 같이 발생가능한 확률을 0-1로 제한을 두지 않습니다. 이렇게 되면 모형을 해석할 때 유의미한 Insight를 얻는 것이 제한됩니다.
[프로빗 모형(Probit)]
프로빗 모형에서, 누적 표준 정규 분포 함수 $\Phi()$를 회귀모형을 추정하는데 활용합니다.
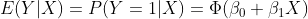
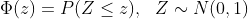
프로빗 모형의 계수 $\beta_1$은 $X$가 한단위 변할 때 $z$의 변화정도와 관련되어 있습니다. $z$와 $X$는 선형관계이지만, $Y$와 $X$는 비선형 관계를 가집니다.
일반화된 Probit 모형은 아래와 같습니다.
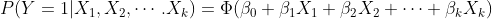
파이썬을 활용하여 Probit 모형을 구현해보겠습니다.
##Probit
from statsmodels.discrete.discrete_model import Probit
X = HMDA["pirat"]
X = sm.add_constant(X)
Y = HMDA["deny_binary"]
denyprobit = Probit(Y, X).fit()
denyprobit.summary()
'''
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -2.1942 0.129 -17.010 0.000 -2.447 -1.941
pirat 2.9679 0.359 8.265 0.000 2.264 3.672
==============================================================================
'''
## 시각화
HMDA["probit"]= denyprobit.predict(X)
plt.plot(HMDA["pirat"],HMDA["deny_binary"] ,"o")
plt.xlim(-0.2, 3.2)
plt.ylim(-0.5,1.5)
plt.xlabel("pirat")
plt.ylabel("deny")
sns.lineplot(data=HMDA, x="pirat", y="probit")
plt.show()
위의 그림에서 보는 것과 같이 Probit 모형은 S-shape을 가지게 됩니다. 이는 누적 표준 정규 분포를 활용하여 Y Value를 표현하기 때문입니다.
pirat이 0.3에서 0.4로 변경될때 Y가 1이될 확률의 변화가 얼마나 일어나는지를 확인해보겠습니다.
## new_data
pirat =np.array([0.3,0.4])
const = np.array([1,1])
X_new = pd.DataFrame([const,pirat]).T
X_new.columns = ["const","pirat"]
denyprobit.predict(X_new).diff()[1]
## 0.060815pirat이 0.3에서 0.4로 올라가면 약 6.2% Y=1일 확률이 높아지는 것을 확인할 수 있습니다.
다음으로는 Race가 어떻게 Mortage 승인 거부 될 확률에 영향을 미치는지를 알아보겠습니다.
## Probit2
HMDA["black"]=HMDA["afam"].apply(lambda x : 1 if x=="yes" else 0)
X2 = HMDA[["pirat", "black"]]
X2 = sm.add_constant(X2)
denyprobit2 = Probit(Y, X2).fit()
denyprobit2.summary()
'''
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -2.2587 0.130 -17.391 0.000 -2.513 -2.004
pirat 2.7416 0.360 7.624 0.000 2.037 3.446
black 0.7082 0.083 8.488 0.000 0.545 0.872
==============================================================================
'''
위의 모형에서 보는 것과 같이 pirat과 black모두 통계적으로 유의했으며, black인 사람들은 Y=1일 확률(Mortage 승인 거부 확률)이 더 높다는 것을 알 수 있습니다. 그렇다면 pirat이 일정할때, black여부에 따른 차이를 분석해보겠습니다.
## new_data
black =np.array([0,1])
pirat =np.array([0.3,0.3])
const = np.array([1,1])
X_new = pd.DataFrame([const,pirat, black]).T
X_new.columns = ["const","pirat","black"]
denyprobit2.predict(X_new).diff()[1]
##0.157813black인 경우에 약 15.8% Y=1일 확률이 높아짐을 알 수 있습니다.
'계량경제학' 카테고리의 다른 글
| Instrumental Variable Regression(도구변수를 활용한 회귀분석) (0) | 2020.11.08 |
|---|---|
| Binary 변수를 가지는 회귀분석(로짓 모형) (0) | 2020.11.02 |
| Panel 회귀모형 (0) | 2020.10.24 |
| 회귀분석의 해석 (0) | 2020.10.18 |
| 회귀분석 with interaction term (0) | 2020.10.12 |