2020. 10. 18. 18:58ㆍ계량경제학
이번 포스팅에서는 앞서 정리하였던 비선형 회귀분석과 상호작용 term을 가지는 회귀분석을 활용하여 여러가지 모형을 수립하고 서로 비교를 통해, 각 변수간의 관계를 분석해보도록 하겠습니다.
먼저 회귀분석 모형수립 및 분석에 들어가기 앞서, 활용하는 변수의 뜻을 다시 한번 정리해보고 가겠습니다.
size = 학생수와 선생님수의 비율(학생수/선생님 수)
score = 시험 점수
lunch = 급식보조를 받는 학생의 비율
enlgish = 영어를 배운 학생들의 비율
income = 수입
이제 위의 변수들을 활용하여, 7가지 모형을 수립하고 비교 분석을 해보도록 하겠습니다. 이를 통해 1) size가 score에 어떻게 영향을 미치고, 2)영어를 배운 학생들의 비율(english)가 어떻게 size가 가지는 영향력을 변화시키는지, 3) size와 score간에 비선형관계가 있는지를 알아보도록 하겠습니다.

## Data load
CASchools = pd.read_csv("CASchools.csv")
CASchools["size"]=CASchools["students"]/CASchools["teachers"]
CASchools["score"]=(CASchools["read"]+CASchools["math"])/2
CASchools["HiSTR"]=CASchools["size"].apply(lambda x : 1 if x>=20 else 0)
CASchools["HiEL"]=CASchools["english"].apply(lambda x : 1 if x>=10 else 0)
## reg model
Score_mod1 = smf.ols("score ~ size +english+ lunch", data=CASchools).fit()
Score_mod2 = smf.ols("score ~ size +english+ lunch+ np.log(income)", data=CASchools).fit()
Score_mod3 = smf.ols("score ~ size +HiEL+ HiEL:size", data=CASchools).fit()
Score_mod4 = smf.ols("score ~ size +HiEL+ HiEL:size+ lunch+np.log(income)", data=CASchools).fit()
Score_mod5 = smf.ols("score ~ size +I(size**2)+ I(size**3)+HiEL+lunch+np.log(income)", data=CASchools).fit()
Score_mod6 = smf.ols("score ~ size +I(size**2)+ I(size**3)+HiEL+HiEL:size+HiEL:I(size**2)+HiEL:I(size**3)+lunch+np.log(income)", data=CASchools).fit()
Score_mod7 = smf.ols("score ~ size +I(size**2)+ I(size**3)+english+lunch+np.log(income)", data=CASchools).fit()Stargazer 패키지를 활용하여 회귀분석 Summary를 한번에 보도록 하겠습니다.
from stargazer.stargazer import Stargazer
stargazer = Stargazer([Score_mod1, Score_mod2,Score_mod3, Score_mod4,Score_mod5, Score_mod6,Score_mod7])
stargaze_html = stargazer.render_html()
f= open("reg_.html", "w")
f.write(stargaze_html)
f.close()html 파일로 입력한 후, html 파일을 열어주면 아래와 같은 표를 확인할 수 있습니다.
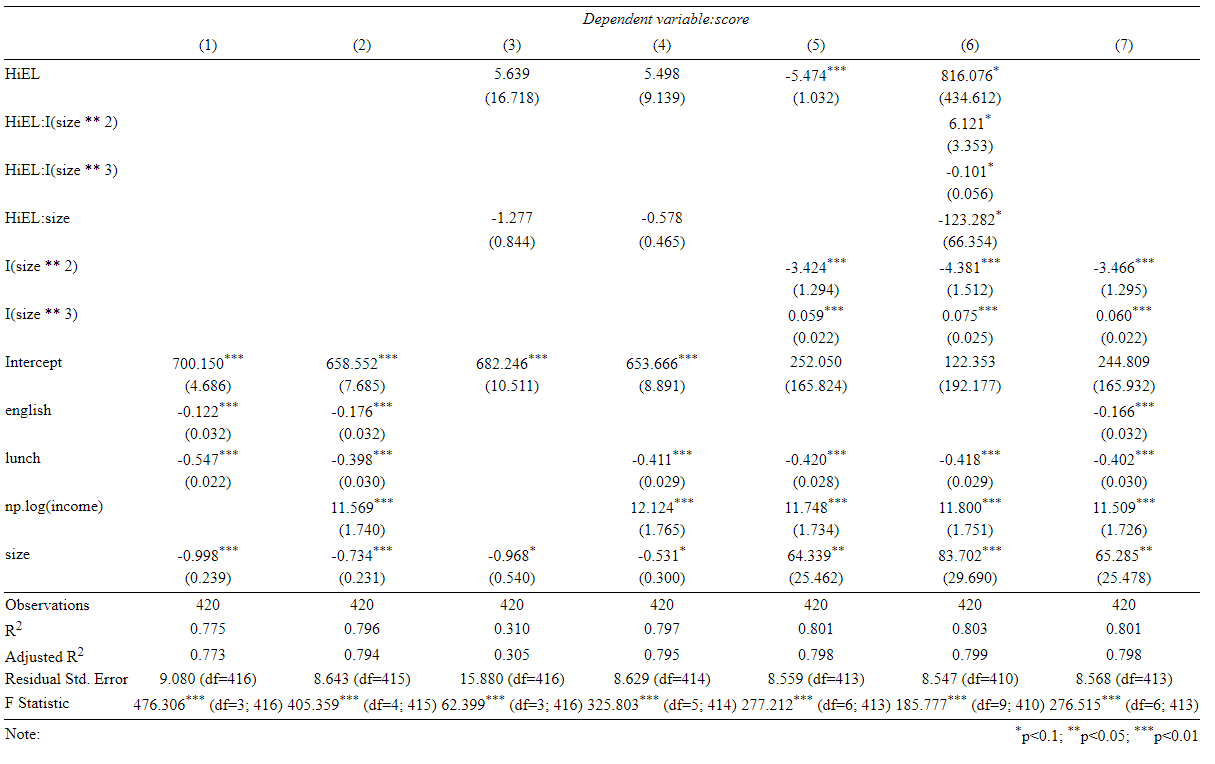
위 결과를 바탕으로 주요 시사점을 정리해보도록 하겠습니다.
1. size는 7가지 모형에서 모두에서 통계적으로 유의하였습니다.
2. 회귀모형 (3), (4)는 size와 HiEL과의 상호작용 효과를 분석 하였습니다 (3),(4)에서 HiEL 더미변수와 size와 HiEL과의 상호작용은 통계적으로 유의하지 않았습니다.
3. 회귀모형 (5)에서는 Cubic term를 추가하였는데, 통계적으로 유의하였습니다. 이는 size와 score간에 비선형적 관계성이 존재함을 나타냅니다.
4. 회귀모형(6)에서는 HiEL*size, HiEL*$size^2$ 과 HiEL*$size^3$의 상호작용관계가 통계적으로 유의하게 나왔습니다. 회귀모형 (3),(4)에서는 통계적으로 유의하지 않게 나왔기 때문에 서로 반대되는 결과를 보여줍니다. F-test를 통해서 검증이 필요할 것 같습니다. 이때 F-test의 귀무가설은 아래와 같습니다.

## F-test
anovaResults = anova_lm(Score_mod5, Score_mod6)
print(anovaResults) ## p-value: 0.248546
p-value 가 0.05 유의수준 보다 높기때문에, 해당 귀무가설을 기각할 수 없게 됩니다. 따라서 통계적으로 상호작용관계가 없다고 해석할 수 있습니다.
5. 결론적으로 우리는 size와 eglish와의 뚜렷한 상호 영향 관계에 대한 분명한 증거를 발견했다고 말하기가 어렵습니다.
위와 같이, 이론적으로는 서로 다른 독립변수가 다른 변수의 Parameter를 추정할 때 영향을 주지 않아야 하지만 현실적으로는 거의 불가능에 가깝습니다. 따라서 엄밀한 증거를 찾을 수 있도록 여려 모형을 수립하여 서로 비교하는 것도 해석의 타당성을 더하는데 활용할 수 있는 주요 방안일 것입니다.
출처: Introduction to Econometrics with R
'계량경제학' 카테고리의 다른 글
| Binary 변수를 가지는 회귀분석(프로빗 모형) (2) | 2020.11.01 |
|---|---|
| Panel 회귀모형 (0) | 2020.10.24 |
| 회귀분석 with interaction term (0) | 2020.10.12 |
| 비선형 회귀모형 > 다항 모형, Log 모형 (0) | 2020.10.04 |
| 회귀분석 가설검정 > F-test (1) | 2020.10.03 |