2020. 9. 10. 22:53ㆍ계량경제학
다중공선성(Multicollinearity)은 다중회귀분석에서 활용된 두 개 이상의 독립변수가 강하게 연관되어 있을 때, 발생하는 문제입니다.
[Perfect Multicollinearity]
만약 두 개 이상의 독립변수 사이가 완벽하게 연관되어 있다면, 즉 한 변수를 다른 변수가 선형결합을 통해서 표현할 수 있다면 Perfect Multicollinearity가 있다고 판단할 수 있습니다. 만약 Perfect Multicollinearity가 발생하게 되면 OLS를 활용하여 계수를 추정할 수가 없게 됩니다.
예를 통해 Perfect Multicollinearity가 발생했을 때 어떤 현상이 일어나는지 알아보겠습니다.
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
from math import sqrt
import random
import scipy.stats as stats
import os
os.chdir("C:/Users/user/Desktop/Python_project/econometrics")
## load the data
CASchools = pd.read_csv("CASchools.csv")
CASchools.head()
## define variable
CASchools["STR"]=CASchools["students"]/CASchools["teachers"]
CASchools["score"]=(CASchools["read"]+CASchools["math"])/2
multi_mod_ = smf.ols("score ~ STR+english",data=CASchools).fit()
multi_mod_.summary()
"""
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 686.0322 7.411 92.566 0.000 671.464 700.600
STR -1.1013 0.380 -2.896 0.004 -1.849 -0.354
english -0.6498 0.039 -16.516 0.000 -0.727 -0.572
"""
CASchools["FracEL"]=CASchools["english"]/100
multi_mod_2 = smf.ols("score ~ STR+english+FracEL",data=CASchools).fit()
multi_mod_2.summary()
"""
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 686.0322 7.411 92.566 0.000 671.464 700.600
STR -1.1013 0.380 -2.896 0.004 -1.849 -0.354
english -0.6497 0.039 -16.516 0.000 -0.727 -0.572
FracEL -0.0065 0.000 -16.516 0.000 -0.007 -0.006
[2] The smallest eigenvalue is 1.74e-30. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
"""
사실 Perfect Multicollinearity가 발생하면, 계수가 추정이 되지 않아야 하는 것이 맞습니다. 다만, R에서는 Na값을 주는데 Python에서는 Na값을 주지 않고 값을 주고 있습니다. 그 대신 " The smallest eigenvalue is 1.74e-30. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular"란 경고문구를 보내줍니다.
회귀분석에서 계수는 아래와 같이 추정됩니다.(Matrix form)
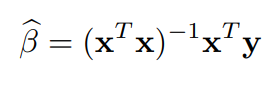
위 식에서 보는것과 같이, 만약에 $(x^Tx)$ 가 역행렬을 구할 수 없다면 이는 계수를 추정할 수 없다는 것입니다. 그런데 input matrix를 이루고 있는 Column들 중 한 Column이 다른 Column에 완벽한 선형결합으로 나타내질 수 있다면 $(x^Tx)$ 는 Determinant가 0이 되고, 역행렬을 구할 수 없게 됩니다.(invertible)
또 다른 Perfect Multicollinearity 예를 살펴보겠습니다.
CASchools["NS"]=CASchools["STR"].apply(lambda x: 0 if x <12 else 1 )
multi_mod_3 = smf.ols("score ~ STR+english+FracEL+NS",data=CASchools).fit()
multi_mod_3.summary()
"""
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 343.0161 3.706 92.566 0.000 335.732 350.300
STR -1.1013 0.380 -2.896 0.004 -1.849 -0.354
english -0.6497 0.039 -16.516 0.000 -0.727 -0.572
FracEL -0.0065 0.000 -16.516 0.000 -0.007 -0.006
NS 343.0161 3.706 92.566 0.000 335.732 350.30
[2] The smallest eigenvalue is 1.04e-30. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
"""위의 예에서는 NS 값이 모두 1이 됩니다. 이는 Intercept의 선형결합으로 나타내짐을 뜻합니다. (Intercept는 Input값이 모두 1인 변수를 OLS로 추정한 것과 같음) Python에서 주는 결과는 단순히 새로운 Intercept는 기존의 Intercept값 686을 절반으로 낮추고, NS에 절반의 영향력을 준 것과 같습니다. Python에서 를 Perfect Multicollinearity여부를 확인할 때는 경고창을 꼭 확인해야 합니다.
[Imperfect Multicollinearity]
Imperfect Multicollinearity는 완전히 선형결합으로 표현될 수 없지만, 그에 가깝게 관계성(Correlation)이 강한 경우입니다. 추정된 계수의 분산은 아래와 같습니다.

만약, $(x^Tx)$ 가 역행렬을 구할 수는 있으나, 역행렬이 구하기 어려운 상태에 가깝다면(Determinant가 0에 가깝다면) 추정된 계수의 Variance가 커지게 될 것이고, 활용된 변수들의 유의성을 확보하기가 어렵게 됩니다. 혹자는 이런한 불완전한 다중공선성은 크게 중요하지 않다고 여기는 사람도 있습니다.
불완전한 다중공선성문제는 수립한 모형의 논리적 타당성의 문제라기 보다는 사용된 데이터와 관련된 문제라고 보는것이 맞는 것 같습니다.
예를 통해 Imperfect Multicollinearity가 발생했을 때 어떤 현상이 일어나는지 알아보겠습니다.
mu_ = np.array([0,0])
cov_ = np.array([[10,2.5],[2.5,10]])
cov_2 = np.array([[10,8.5],[8.5,10]])
#Case1
coeff=[]
for i in range(10000):
X_1 = np.random.normal(0, 10, 50)
X_2 = np.random.normal(0, 10, 50)
X=np.column_stack([X_1, X_2])
X =sm.add_constant(X)
u = np.random.normal(0,5, size=50)
Y = 5 + 2.5*X[:,1]+X[:,2]+u
reg_=sm.OLS(Y, X).fit()
coeff.append(reg_.params[1:])
#Case2
coeff_mul_25=[]
for i in range(10000):
X = np.random.multivariate_normal(mu_, cov_, 50)
X =sm.add_constant(X)
u = np.random.normal(0,5, size=50)
Y = 5 + 2.5*X[:,1]+X[:,2]+u
reg_=sm.OLS(Y, X).fit()
coeff_mul_25.append(reg_.params[1:])
#Case3
coeff_mul_85=[]
for i in range(10000):
X = np.random.multivariate_normal(mu_, cov_2, 50)
X =sm.add_constant(X)
u = np.random.normal(0,5, size=50)
Y = 5 + 2.5*X[:,1]+X[:,2]+u
reg_=sm.OLS(Y, X).fit()
coeff_mul_85.append(reg_.params[1:])
coeff = pd.DataFrame(coeff)
coeff_mul_25 = pd.DataFrame(coeff_mul_25)
coeff_mul_85 = pd.DataFrame(coeff_mul_85)
coeff.var() #([0.00532848, 0.00544153])
coeff_mul_25.var() #([0.05701568, 0.05974069])
coeff_mul_85.var() #([0.19373028, 0.19283941])Case1에서는 두 Input 변수에 Covariance를 고려하지 않고 별도 Random으로 Sampling을 했고 Case2에서는 Cov($X_1$, $X_2$)를 2.5로 설정하여 다변량 정규분포로 Sampling을 했으며, Case3에서는 Cov($X_1$, $X_2$)를 8.5로 하여 Sampling을 했습니다.
그 결과 Cov($X_1$, $X_2$)가 커질수록 분산이 커짐을 확인할 수 있습니다.
참고:
'계량경제학' 카테고리의 다른 글
| 비선형 회귀모형 > 다항 모형, Log 모형 (0) | 2020.10.04 |
|---|---|
| 회귀분석 가설검정 > F-test (1) | 2020.10.03 |
| 회귀분석 가설검정 (0) | 2020.09.17 |
| VIF(분산팽창요인), 결정계수 (0) | 2020.09.13 |
| Omitted Variable Bias (0) | 2020.09.10 |