2025. 5. 2. 17:15ㆍ계량경제학
많은 시계열 데이터들이 비정상(Non-stationary) 특성을 나타냅니다. 이러한 비정상 시계열을 전통적 회귀분석으로 하면 변수들간에 실제 관계가 없더라도 단순히 시간에 따라 움직이기만 해도 회귀분석상에서는 관계가 있게 나올 수 있습니다. 이러한 현상은 Spurious regression문제를 발생시킬 수 있습니다.
따라서 이러한 문제를 해결하고자 비정상 시계열의 데이터 간의 진정한 관계를 살펴보고자 할때 활용할 수 있는 모형중에 하나가 오차수정모형입니다.
오차수정모형(ECM)은 비정상(non-stationary) 시계열 데이터 간의 장기 균형 관계와 단기 동적 조정 과정을 설명하는 모델입니다. 이 모델은 공적분(cointegration) 관계가 있는 변수들 간의 동적 관계를 분석하는 데 사용됩니다.
공적분은 시계열 데이터들이 비정상(Non-stationary) 특성을 나타냅니다. 이러한 비정상 시계열을 전통적 회귀분석으로 하면 변수들간에 실제 관계가 없더라도 단순히 시간에 따라 움직이기만 해도 회귀분석상에서는 관계가 있게 나올 수 있습니다. 이러한 현상은 Spurious regression문제를 발생시킬 수 있습니다.
따라서 이러한 문제를 해결하고자 비정상 시계열의 데이터 간의 진정한 관계를 살펴보고자 할때 활용할 수 있는 모형중에 하나가 오차수정모형입니다.
오차수정모형(ECM)은 비정상(non-stationary) 시계열 데이터 간의 장기 균형 관계와 단기 동적 조정 과정을 설명하는 모델입니다. 이 모델은 공적분(cointegration) 관계가 있는 변수들 간의 동적 관계를 분석하는 데 사용됩니다. 공적분(https://direction-f.tistory.com/125)은 장기균형관계가 있음을 나타내며, 오차수정모형은 이러한 장기균형관계가 이탈됐을때 각 변수가 얼마나 균형으로 빠르게 다시 복귀하는지를 살펴볼 수 있습니다.
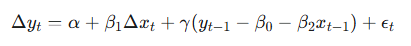
이중에서 아래 수식이 오차수정항으로 불리며 장기적 균형을 나타냅니다.(각 계수는 Cointegraion으로 추정)

γ (gamma)는 여기서 균형회복 속도를 나타내며, β 는 변수 X가 Y에 미치는 단기영향을 나타냅니다.
이제 실제 예시를 통해 ECM을 살펴보겠습니다.
일단 가상의 데이터를 먼저 생성해보겠습니다.
import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller, coint
from statsmodels.tsa.ardl import UECM
# 예시 데이터 생성
np.random.seed(1)
n_samples = 100
income = np.cumsum(np.random.randn(n_samples)) + 50
spending = 0.8 * income + np.random.randn(n_samples) * 5
data = pd.DataFrame({'Income': income, 'Spending': spending})그 다음 ADF 테스트를 통해 비정상성을 가지는지 확인합니다. ECM에 적합하기 위해서는 공적분 관계가 있어야 하고 공적분 관계는 비정상성 시계열들의 결합의 정상성이기 때문에 ADF 테스트결과 비정상성을 가진 시계열이라고 나와야 합니다.
result = adfuller(data['Income'].values)
print(f'ADF Statistic: {result[0]:.4f}')
print(f'p-value: {result[1]:.4f}')
"""
ADF Statistic: -0.7147
p-value: 0.8429 -> 귀무가설을 기각하지 못하여 비정상성
"""
result = adfuller(data['Spending'].values)
print(f'ADF Statistic: {result[0]:.4f}')
print(f'p-value: {result[1]:.4f}')
"""
ADF Statistic: -1.8063
p-value: 0.3773 -> 귀무가설을 기각하지 못하여 비정상성
"""이후 공적분 테스트를 수행합니다. 공적분 결과 두 변수간에 공적분 관계가 있음이 나타났습니다.
result_coint = coint(data["Spending"], data["Income"])
print('Cointegration p-value:', result_coint[1])
"""
Cointegration p-value: 0.00010847779294609566
"""이제 공적분 관계의 회귀식을 추정합니다. 위에서 ECM에서 설명한것과 같이 오차수정항에 해당 회귀식을 활용하기 위함입니다.
X_with_const = sm.add_constant(data["Income"])
coint_model = sm.OLS(data["Spending"], X_with_const)
coint_results = coint_model.fit()
print(coint_results.summary())
print(f"상수항: {coint_results.params['const']:.4f}")
print(f"X 계수: {coint_results.params['Income']:.4f}")이제 ECM 모형을 추정해보겠습니다.
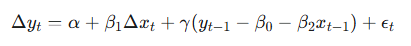
해당 수식에 맞게 데이터를 가공한후 OLS로 적합합니다.
## ECM 데이터 가공
data['dY'] = data['Spending'].diff()
data['dX'] = data['Income'].diff()
data['EC'] = data['Spending'].shift(1) - (coint_results.params['const'] + coint_results.params['Income'] * data['Income'].shift(1))
# ECM 모델 적합
X_ecm = sm.add_constant(data[['dX', 'EC']].dropna())
y_ecm = data['dY'].dropna()
model = sm.OLS(y_ecm, X_ecm)
results = model.fit()# 결과 출력
print("\nECM 모델 결과:")
print(results.summary())
# 결과 해석
print("\n결과 해석:")
print("1. 단기 영향 (β):")
print(f" - X의 현재 변화가 Y에 미치는 영향: {results.params['dX']}")
print(f" - p-value: {results.pvalues['dX']}")
print("\n2. 오차수정계수 (γ):")
print(f" - 장기 균형에서 벗어난 편차의 조정 속도: {results.params['EC']}")
print(f" - p-value: {results.pvalues['EC']}")
"""
결과 해석:
1. 단기 영향 (β):
- X의 현재 변화가 Y에 미치는 영향: 1.5188630484002266
- p-value: 0.006372307452717308
2. 오차수정계수 (γ):
- 장기 균형에서 벗어난 편차의 조정 속도: -1.1167648802661265
- p-value: 2.2216056604163517e-18
"""오차수정계수 (γ) 가 -1.11로 나왔으며, 이는 장기균형에서 편차가 발생했을 때 -1.11만큼 다시 Y값이 낮아짐을 나타냅니다. 만약 -0.7이면 그 조정정도가 더 약한것이고 -2.0이었으면 그 조정정도가 강하다라고 볼수 있습니다.
'계량경제학' 카테고리의 다른 글
| 벡터오차수정모형 (VECM, Vector Error Correction Model) (1) | 2025.05.05 |
|---|---|
| 공적분(Cointegration) (2) | 2025.04.30 |
| Granger Causality(그레인저 인과관계) (1) | 2025.04.28 |
| VAR(Vector Autoregressive Models) (1) | 2024.06.17 |
| 시계열(Time series) > Break (0) | 2021.01.05 |